Portfolio 2 IA

Intruduction

Welcome to a journey through the world of search algorithms! In this guide, we’ll explore various strategies that computers use to search and solve problems, making things work efficiently and intelligently.

First, we’ll look at Open-Loop and Closed-Loop systems, explaining their basic differences and how they operate. Next, we’ll dive into Algorithm Searches, discussing how algorithms go through data to find what we’re looking for.

We’ll also touch on Heuristic Functions, the smart shortcuts that help algorithms find solutions quicker. Then, we’ll explore the concept of Searching in Complex Environments, where algorithms face and navigate through challenging and multifaceted tasks.

Lastly, we’ll delve into Genetic Algorithms, a fascinating approach inspired by nature and evolution, used to find solutions in various complex problems.

In each part of this guide, we aim to present these concepts in a clear and simple way, making the fascinating world of search algorithms accessible and understandable to everyone. Let’s begin this exploratory journey!

Open-Loop and Closed-Loop

1. Open-Loop:
   • In an open-loop system, control does not depend on feedback from the system’s output.
   • The system’s actions are independent of its output.
   • The system follows predefined instructions and does not adjust based on what’s happening in the environment or the system’s output.
   • For example, a production line where the implementation of the product parts is independent of the previous process; the machines will just continue operating regardless of the previous process..
2. Closed-Loop:
   • In a closed-loop system, control is exerted based on feedback from the output.
   • The system constantly monitors the output and makes adjustments to ensure the desired output is achieved.
   • This allows the system to adapt to changes in conditions and correct any deviations from the desired output.
   • Using the example from the text about “Computer-Assisted Surgery Robots”, the robotic system collects real-time information about the patient’s anatomy and continuously adapts to the surgeon’s actions, ensuring accurate and safe surgery.

Algorithms Search

Blind Search Algorithms (Uninformed Search)

Blind search algorithms, also known as uninformed search algorithms, explore the search space without any knowledge about the problem other than its definition. These algorithms do not have any information on whether a move gets them closer to a solution or not. They work by exhaustively trying all possibilities until the solution is found or all options are tried.

Characteristics of Blind Search Algorithms:

• They do not use any problem-specific knowledge.
• They rely on a brute-force approach to explore all possible states.
• They can be less efficient, especially for large search spaces.

Breadth-First Search (BFS)

Breadth-First Search is a simple strategy where the root node is expanded first, then all the successors of the root node are expanded next, followed by their successors, and so on. In BFS, nodes are expanded according to the number of moves made from the start node.

• Advantages:
  • Finds the shortest path to the goal if there is one.
  • Suitable for searching wide trees or graphs.
• Disadvantages:
  • Can consume a lot of memory, especially if the branching factor is high.

Depth-First Search (DFS)

Depth-First Search explores as far as possible along each branch before backtracking. It starts from the root and goes as deep as possible before backtracking.

• Advantages:
  • Uses less memory than BFS.
  • Can be simpler to implement (using recursion or a stack).
• Disadvantages:
  • Might not find the shortest path.
  • Can get stuck in infinite loops if there are cycles in the search space.

Best First Search

Best First Search is a search algorithm that explores a graph by selecting the next node based on a heuristic. The heuristic is an estimate of the cost from the current node to the goal.

• Advantages:
  • Uses problem-specific knowledge, which can make it more efficient.
  • Flexible, as different heuristics can be used for different problems.
• Disadvantages:
  • The quality of the solution depends on the heuristic.
  • Does not always guarantee the shortest path.

Uniform Cost Search (UCS)

Uniform Cost Search is a search algorithm that expands the node with the lowest path cost. Instead of expanding nodes in the order they are discovered (as in BFS) or by depth (as in DFS), UCS selects nodes based on their path cost from the start node.

• Advantages:
  • Always finds the least-cost path.
  • Can handle varying path costs (unlike BFS).
• Disadvantages:
  • Can be slower than other methods, especially if the branching factor is high.

Informed Search Algorithms (Heuristic Search)

In contrast, informed search algorithms, or heuristic search algorithms, use problem-specific knowledge to make decisions about which branch to explore next. This knowledge often comes in the form of a heuristic, which provides an estimate of how close a state is to a solution. By using heuristics, these algorithms can find solutions more efficiently than blind search algorithms.

Characteristics of Informed Search Algorithms:

• They use problem-specific knowledge or heuristics.
• They aim to prioritize paths that are more likely to lead to a solution.
• They are generally more efficient than blind search algorithms for many problems.

Greedy Best-First Search (GBFS)

Greedy Best-First Search (GBFS) is an informed search algorithm that uses a heuristic function to predict the cost from the current node to the goal. It prioritizes nodes based on this heuristic, aiming to find the most promising path by choosing the node that appears closest to the goal.

• Advantages:
  • Can be more efficient than uninformed search algorithms since it uses problem-specific knowledge.
  • Often explores fewer nodes than algorithms like Breadth-First Search.
• Disadvantages:
  • Does not always guarantee the shortest or least-cost path.
  • The efficiency and effectiveness heavily depend on the quality of the heuristic.

A* Search

A* Search is a widely used informed search algorithm that combines the features of uniform-cost search and GBFS. It considers both the cost to reach the current node and the estimated cost from the current node to the goal. The formula for A* is: f(n) = g(n) + h(n), where g(n) is the cost to reach the node, and h(n) is the heuristic estimate to the goal.

• Advantages:
  • Guarantees the shortest path if the heuristic is admissible (never overestimates the true cost) and consistent (satisfies the triangle inequality).
  • Tends to be more efficient than other search algorithms, especially with a good heuristic.
• Disadvantages:
  • Like GBFS, its performance can be heavily influenced by the heuristic chosen.
  • Might consume more memory than other methods if many nodes have to be stored.

Heuristic Functions

Comparison of search costs

A heuristic function, often simply called a “heuristic”, is a method or formula that estimates the cost from a given state or node in a search tree to a goal state. The primary purpose of a heuristic is to guide search algorithms, particularly informed search algorithms, towards the most promising paths, and away from less promising ones. This makes it possible for the algorithm to find solutions more efficiently, without exhaustively searching all possibilities.

Key Points:

1. Estimation: Heuristics do not provide the exact cost but an estimation of it. The better the estimation, the more effectively the search algorithm can operate.

2. Admissibility: A heuristic is said to be admissible if it never overestimates the actual cost to reach the goal. Admissibility ensures that algorithms like A* Search will find the optimal solution.

3. Consistency (or Monotonicity): A heuristic is consistent if the estimated cost from the current node to the goal is less than or equal to the cost from the current node to any successor node plus the estimated cost from the successor to the goal.

4. Problem-Specific: Heuristics are often tailored to specific problems. The effectiveness of a heuristic can greatly vary based on the problem domain.

5. Trade-offs: While heuristics help in speeding up the search process, they can sometimes lead to suboptimal solutions, especially if the heuristic is not well-designed for the problem.

Diagram:

Here’s a simple representation of how a heuristic function works in the context of a search:

Start Node (A)   ----->   Intermediate Node (B)   ----->   Goal Node (C)
       |                           |                           |
 Heuristic h(A)              Heuristic h(B)              Heuristic h(C) = 0

In this diagram:

• h(A): Estimated cost from node A to the goal.
• h(B): Estimated cost from node B to the goal.
• h(C): Since node C is the goal, the heuristic value is 0.

In practice, informed search algorithms will use these heuristic values to prioritize which nodes to explore next.

Searching in Complex Environments

• So far, we have been concerned with finding a path in the search space.
• Sometimes, we are only concerned with the final state, and not with the path to get there.
• This other type of approach is used in fields such as: integrated circuit design, factory floor layout, automatic programming, telecommunications network optimization, crop planning, and portfolio management.

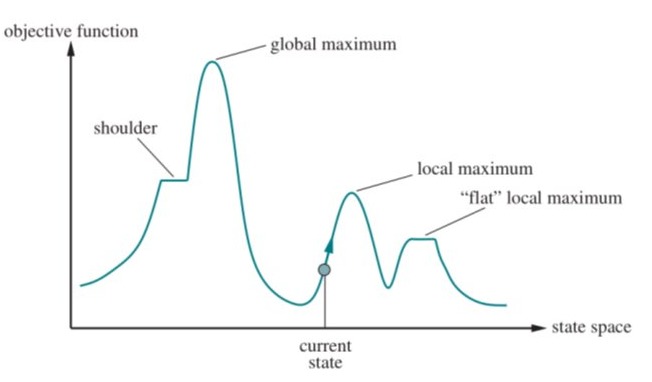
Local Search

• If the elevation corresponds to the objective function, the goal is to find the highest peak, and the process is called hill climbing.

• If the elevation corresponds to the cost, the goal is to find the lowest valley, and the process is called gradient descent.

Local Search

Genetic Algorithms (Evolutionary algorithms)

Genetic Algorithms (Evolutionary algorithms)

• There is a population of individuals (states);
• The fittest individuals (highest value of a function) produce descendants (successor states) that populate the next generation through a process called recombination;
• Mutation can occur during recombination.

Genetic Algorithms - Parameters

• Population size: How many examples or samples do we have;
• Representation of each individual (DNA): e.g., positions on a chessboard;
• Number of parents (p): the most common case p = 2;
• Selection: Process of selecting individuals who became the parents;
• Recombination procedure: random, how much from each parent?
• Mutation rate: random and what is the probability?
• New generation: discard? Are parents kept in the new generation?

Discussion

Genetic algorithms (GAs) are a class of evolutionary algorithms inspired by the process of natural selection. They operate by maintaining a population of potential solutions (individuals) and iteratively applying genetic operations such as selection, recombination (crossover), and mutation to generate new individuals (offspring).

• Population and Representation: The population consists of a set of individuals, each representing a possible solution. The representation is how each solution is encoded, and it can be in various forms such as binary strings or as positions on a chessboard.

• Selection: GAs use a selection process where individuals are chosen to be parents based on their fitness values. The fitter individuals have a higher chance of being selected for reproduction.

• Recombination and Mutation: In recombination, genetic material from parents is combined to create offspring, introducing diversity. Mutation introduces further diversity by making small random changes to an individual’s representation.

• New Generation: After generating the offspring, a decision is made whether to keep or discard the parents in the new generation, ensuring that the population size remains constant.

Genetic algorithms are heuristic search algorithms that are good at exploring a vast search space and are used in optimization and search problems where the landscape is complex and multi-modal. They are particularly useful in scenarios where the solution space is large, complex, and poorly understood, and where an exact solution is not mandatory. The parameters of a genetic algorithm, such as the size of the population, mutation rate, and recombination strategy, need to be carefully chosen and tuned to suit the specific problem being solved.

Aerospace Engineering

Example in the field of Optimization in Engineering Designs:

In aerospace engineering, genetic algorithms can be used to optimize the design of aircraft components or even entire aircraft configurations. Engineers aim to design aircraft that are lightweight yet durable, fuel-efficient, and able to meet specific aerodynamic performance criteria.

For example, a GA could be applied to optimize the shape and structure of an aircraft wing. The algorithm would start with a population of different wing designs, each represented with specific parameters such as wing length, shape, angle, and other aerodynamic variables.

• Selection: Designs are evaluated based on objective functions related to aerodynamic efficiency, structural integrity, and weight. The best-performing designs are selected to create a new generation of wing designs.

• Crossover and Mutation: The selected designs undergo crossover and mutation, creating a variety of new wing shapes and configurations. This introduces diversity and enables the exploration of new design possibilities.

• Evaluation and Iteration: The new generation of designs is evaluated, and the process is repeated for several iterations. Over time, the GA converges towards optimal or near-optimal wing designs that meet the desired performance criteria.

By using a GA, engineers can explore a vast design space and find innovative solutions that might not be discovered through traditional engineering design methods. This application of GAs helps in pushing the boundaries of aerospace engineering by facilitating the discovery of more efficient and effective aircraft designs.

Contributions

In this section, we will explore various real-world applications from different fields discussed earlier. Through practical examples, we aim to elucidate the significant impact and contributions of these concepts in everyday scenarios and professional domains.

Example of Open-Loop and Closed-Loop Aplication

Example of a Closed Loop System Aplication

A sophisticated closed loop control system usually includes one or multiple feedback loops.

These feedbacks can include throughput time, capacity utilization, disruptions, scraps, and many more. And the information it includes do not limited to machines and processes but also employees, such as their qualifications, professions, and roles. Usually, these feedbacks are processed mainly by a Shop Floor data collection (SFDC) system.

Shop Floor Data Collection system is the foundation of a Closed Loop Production Control System that collects workers’ feedback and input through shop floor terminals and machines via smart sensors.1

Example of an Open Loop System Aplication

A straightforward example of an open loop control system is a traditional toaster. The user of a toaster will only know when it starts and finishes toasting, with little control over the input (2 slices of bread) as well as the process (Time, temperature, and more).1

Example of Algorithms Search Aplication

Shortest Path and Minimum Spanning Tree for unweighted graph:

In an unweighted graph, the shortest path is the path with the least number of edges. With Breadth First, we always reach a vertex from a given source using the minimum number of edges. Also, in the case of unweighted graphs, any spanning tree is Minimum Spanning Tree and we can use either Depth or Breadth first traversal for finding a spanning tree. 2

How does it work ?

The Minimum Spanning Tree (MST) is a tree that spans all the vertices in a graph, ensuring that the total edge weight is minimized. However, in the case of an unweighted graph, where all edge weights are equal, finding the MST simplifies to finding a spanning tree of the graph. We can use Breadth-First Search (BFS) or Depth-First Search (DFS) to find a spanning tree, and thus solve the MST problem for an unweighted graph.

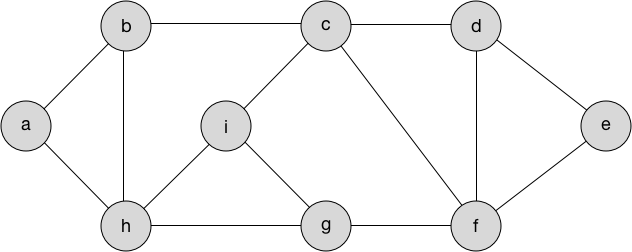Graph 3

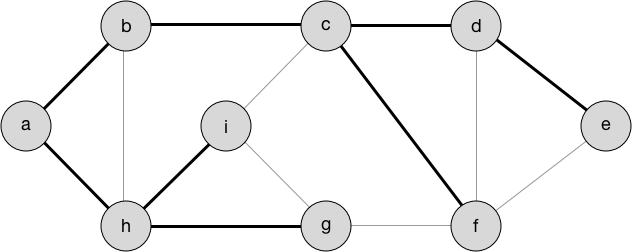Minimum Spanning Tree 3

Using Breadth-First Search (BFS)

BFS explores a graph level by level, visiting all the neighbors of a node before moving on to their neighbors. To find a spanning tree:

1. Initialize: Start from any vertex as the root and mark it as visited.
2. Exploration: Explore the adjacent vertices of the current vertex. Add the edge to the spanning tree and mark the vertex as visited.
3. Queue Management: Maintain a queue of visited vertices. Dequeue a vertex, and repeat the exploration step for unvisited adjacent vertices.
4. Termination: Continue the process until all vertices are visited.

func breadthFirstSearchMinimumSpanningTree(graph: Graph, source: Node) -> Graph {
  let minimumSpanningTree = graph.duplicate()

  var queue = Queue<Node>()
  let sourceInMinimumSpanningTree = minimumSpanningTree.findNodeWithLabel(source.label)
  queue.enqueue(sourceInMinimumSpanningTree)
  sourceInMinimumSpanningTree.visited = true

  while let current = queue.dequeue() {
    for edge in current.neighbors {
      let neighborNode = edge.neighbor
      if !neighborNode.visited {
        neighborNode.visited = true
        queue.enqueue(neighborNode)
      } else {
        current.remove(edge)
      }
    }
  }

  return minimumSpanningTree
}

Reference - 3

Using Depth-First Search (DFS)

DFS explores a graph by going as deep as possible along each branch before backtracking.

1. Initialize: Start from any vertex as the root, mark it as visited.
2. Exploration: Explore an adjacent unvisited vertex, add the edge to the spanning tree, and mark the vertex as visited.
3. Recursion/Stack Management: Recursively repeat the exploration step. If no unvisited adjacent vertices remain, backtrack using the call stack or explicitly using a stack.
4. Termination: Continue until all vertices are visited.

Example of Genetic Algorithms (Evolutionary algorithms) Aplication

Google’s DeepMind - DeepMind, a subsidiary of Google, has utilized genetic algorithms in its research on artificial intelligence. One notable example is the AlphaFold project, where DeepMind used GAs to develop a groundbreaking protein-folding algorithm. The algorithm accurately predicted the 3D structures of proteins, which is crucial for understanding their functions and has implications in drug discovery and disease research.4

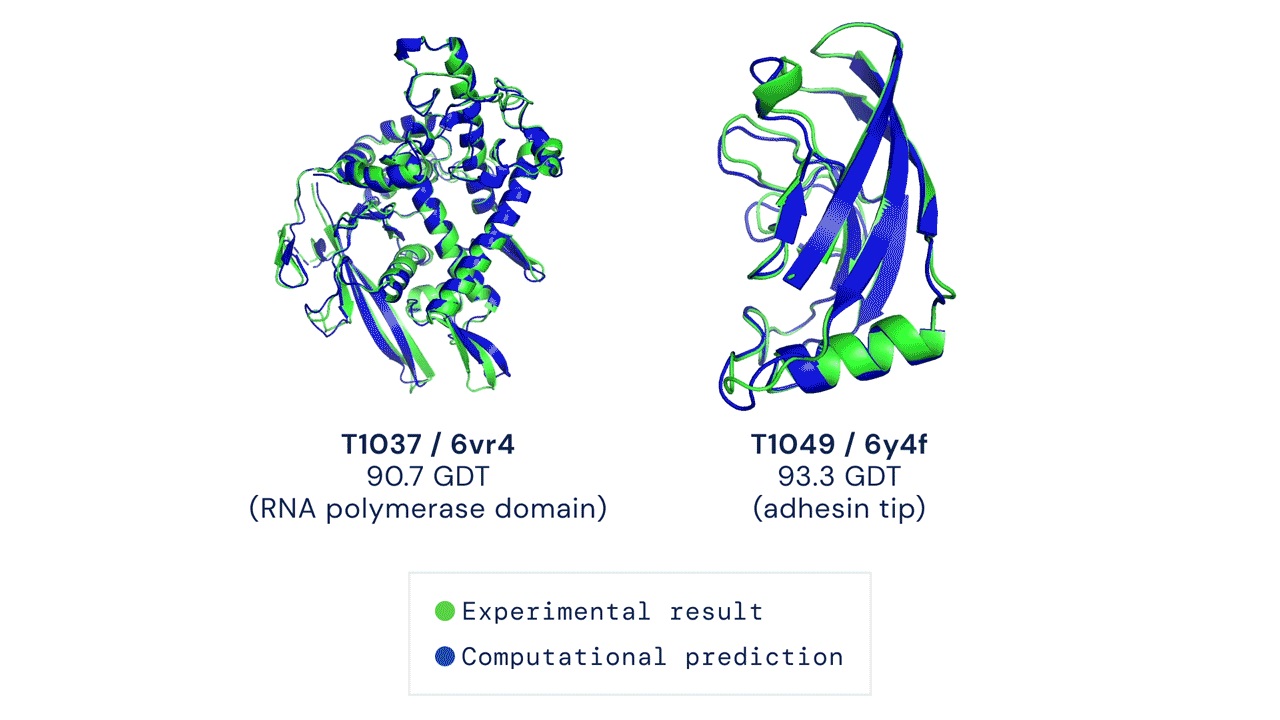3D structures of proteins 5

If you want to know more i highly recommend you to read this article : 6

Conclusion

In conclusion, the exploration of various search strategies such as Open-Loop and Closed-Loop systems, Algorithm Searches, Heuristic Functions, Searching in Complex Environments, and Genetic Algorithms, elucidates the diversity and richness of approaches in computational problem-solving and optimization. Open-Loop and Closed-Loop systems establish the foundational strategies, offering simplistic yet effective approaches for a plethora of applications. Algorithm Searches and Heuristic Functions reveal the power of structured exploration and informed decision-making, enabling enhanced performance and efficiency in finding solutions. The journey through Searching in Complex Environments unveils the robustness and adaptability of algorithms, demonstrating their prowess in navigating through multifaceted challenges. Genetic Algorithms embody the essence of evolutionary inspiration, opening doors to innovative solutions in various complex problems.

Each strategy and algorithm bring unique contributions, showcasing the adaptability, efficiency, and ingenuity of computational methodologies. Their diverse applications across numerous domains underscore the indispensable role they play in technological advancements and problem-solving in today’s dynamic and complex world.Also, understanding and leveraging these various search strategies stand paramount in harnessing the full potential of computational intelligence to navigate the intricate landscapes of problems and challenges in various fields.

References

• Professor’s slides and class material
• Open AI, GPT-3.5, Bing AI, Bard AI (Used to improve the structure of the text, correct grammar and syntax)
• 1 - https://planeus-solutions.com/blog/en/closed-loop-vs-open-loop-production-control-system/
• 2 - https://www.geeksforgeeks.org/applications-of-breadth-first-traversal/
• 3 - https://aquarchitect.github.io/swift-algorithm-club/
• 4 - https://www.spiceworks.com/tech/artificial-intelligence/articles/
• 5 - https://piip.co.kr/en/blog/alphafold-protein-structure-prediction-importance-1
• 6 - https://www.nature.com/articles/s41586-021-03819-2